内容目录
题目
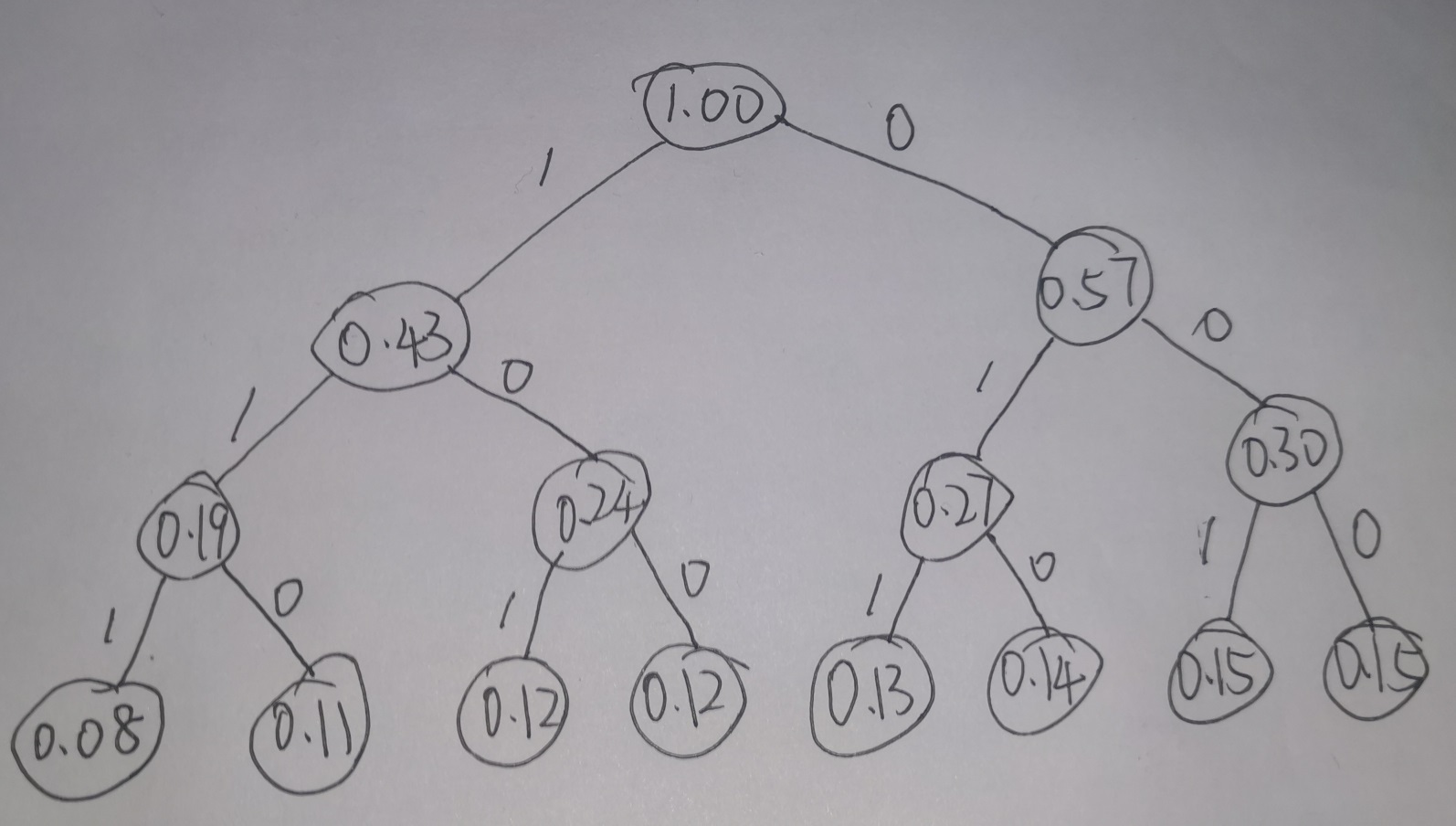
某机8条指令的使用频率为
- 0.12
- 0.08
- 0.11
- 0.14
- 0.15
- 0.15
- 0.12
- 0.13
求出哈夫曼编码的平均码长,并画出哈夫曼树。
分析
本题主要考察哈夫曼编码,哈夫曼树构造过程和码长计算公式。
哈夫曼编码
哈夫曼树
码长
解答
哈夫曼编码是一种用于无损数据压缩的熵编码算法,其中较频繁出现的项目使用较短的编码,而较少出现的项目使用较长的编码。
以下是已知使用频率的8条指令的哈夫曼编码的生成过程:
步骤1:根据给出的频率,将所有的指令列出,并排序,频率从小到大为:0.08, 0.11, 0.12, 0.12, 0.13, 0.14, 0.15, 0.15。
步骤2:选择两个频率最低的,将它们组合成一个新的节点,新的频率为这两个频率的和。如此,最小的两个频率为0.08和0.11,组合后新的频率为0.19。
步骤3:从列表中删除原先的两个频率,并将新的频率加入列表,然后再次排序。此时频率从小到大为:0.12, 0.12, 0.13, 0.14, 0.15, 0.15, 0.19。
步骤4:再次选择频率最小的两个节点,将它们组合,直到所有指令都组合在一个树中,这个树就是哈夫曼树。每一次选择都让编码的长度尽可能短。
通过上述步骤,你可以得到每个指令的哈夫曼编码,哈夫曼编码的平均码长就是每个指令的频率乘以其哈夫曼编码的长度的总和。
计算机系统结构-哈夫曼编码和哈夫曼树