1、概念
渐进符号是对算法运行时间的一种估计,而不是精确的时间。使用渐进符号来估计当输入规模变大时,用一个确定的算法来解决一个问题是否可行,这里的可行是指时间上是否可行。
渐进符号有三个,以下为三个渐进符号:
- big-O: 最坏运行时间
- big-Ω:最好运行时间
- big-Θ:介于两者之间,取两者的交集
渐进符号是对算法运行时间区间的度量,他们之间的关系应该是big-Ω<=big-Θ<=big-O。
1.1、为什么是估计而不是精确时间?
一句话总结:精确时间计算太复杂了,不好做。
因为计算精确时间太复杂,主要因素如下(软件和硬件):
- 算法的运行时间依赖于编程语言
- 算法的运行时间依赖于编译器
- 算法的运行时间依赖于处理器或硬件
- 其他因素
以上这些因素会导致评估精确运行时间的复杂性,因为这些因素都是变量,不同的编程语言、编译器、处理器和其他因素对同一算法的代码编写、编译及优化、处理器的执行是不一样的。在算法设计的及分析时,如果需要把所有的编程语言、编译器、处理器和其他因素都考虑进来,那么算法设计及分析就会非常复杂。
基于以上问题,算法设计和分析需要一个常量,这个常量的意思就是:在这个算法中,无论外部环境(编程语言、编译器、处理器和其他因素)如何改变,算法不变的是什么。算法不变的内容是算法时间分析的一个核心。
1.2、算法分析应该关注什么?
一句话总结:主要关注输入大小和输入的增长,其他因素都视为一个常数。
- 函数输入大小
这个比较容易理解,因为如果任何算法的输入只要足够小,那么这些算法的运行时间都很快,所以输入大小是评判一个算法运行时间的重要维度。 - 函数输入的增长
只关注一些固定大小的输入也不行,因为输入一直会改变,会变大会变小,变小了当然好,因为确定的算法可以处理当前不变的大小,那么处理更小的输入肯定没问题。那如果输入一直在变大,变大一直变成无穷大(夸张手法),那么这个确定的算法在这种情况下运行时间是如何改变的的?
看下图(图片来源于:可汗学院)

这张图是对应的函数是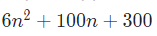
,图中红线的增长趋势远大于蓝线,那么就可以说这个算法的运行时间是n的平方,舍掉了系数6和100n+300两项,之所以可以舍掉这两项是因为我们假设n的数字足够大。什么是足够大?简单把n当成无穷大就可以了。
下图是对n的平台系数的改变的图(图片来源于:可汗学院):
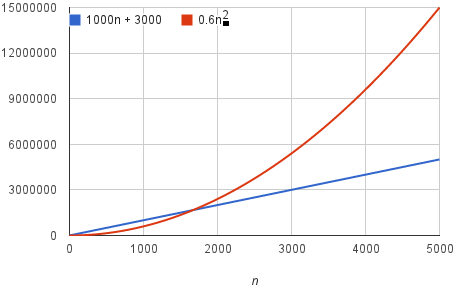
从上图可以看出虽然刚开始的时候红线低于蓝线,但是到达了大概1800及以后,红线的增长趋势开始明显的比蓝线大了,所以常量系数并不影响对增长趋势的评估可以舍弃。
2、big-O 渐进上界
一句话总结:big-O用来描述算法最坏运行时间的,算法的最长运行时间
big-O是对算法最坏运行时间的描述,是为了让人了解算法在一些特殊情况下最大运行的时间。
如果说算法运行时间是O(f(n)),这其实表示在n足够大时,算法的最大运行时间是有一个常量k使得最大运行时间k*f(n)为算法的最大运行时间。
如下图(图片来源于:可汗学院):
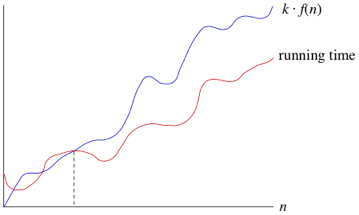
2.1、big-O局限性
big-O符号不能提供算法运行时间的下限,所以需要Ω符号。
3、big-Ω 渐进下界
一句话总结:big-O用来描述算法最好运行时间的,算法的最短运行时间
big-Ω是对算法最好运行时间的描述。因为有时候我们想要知道一个算法最小运行时间。
如下图(图片来源于:可汗学院):
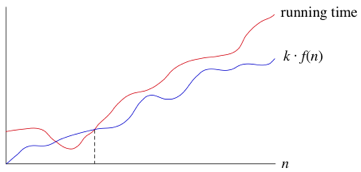
3.1、怎么样来理解和计算big-Ω
一些算法可以在一些特殊的输入下在Ω(1)的运行时间内完成,我也可以说这些算法的最小运行时间是Ω(1),但是不精确。
举例:假设你银行卡里有100块钱,那么你说我的银行卡里面最少有1块钱也是对的,但是并不精确。
所以算法在给出Ω时都需要计算出一个尽可能精确的Ω运行时间。
举例:你可以说我的银行卡里面最好有99.999999…块钱或者说我的银行里有100块钱。
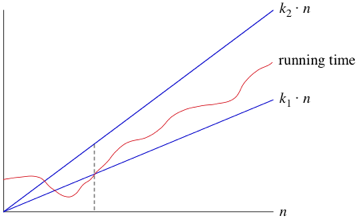
4、big-Θ 渐进紧确界
一句话总结:big-Θ既可以描述上界又可以描述下届,其实就是找一个函数,如果把这个函数塞到Ω和O之间就可以了
当用Θ(n)来描述算法运行时间时,Θ (n)表示该算法运行时间为:最小运行时间是k1*n,最大运行时间是k2*n,其中k1和k2是常数。
如下图(图片来源于:可汗学院):
5、总结
- 算法分析时不要考虑一些外部变量,如编程语言、编译器、处理器和其他因素,聚焦于算法本身上的“不变量”
- 在得到算法函数后,可以通过舍弃掉小项和常量系数,来简化表示
- big-O 用来描述最坏运行时间
- big-Ω用来描述最好运行时间
- big-Θ既可以描述最好又可以描述最坏运行时间
6、参考
- 可汗学院https://www.khanacademy.org/computing/computer-science/algorithms/asymptotic-notation/a/asymptotic-notation
- 离散数学及其应用第六版
- 算法导论 第三版